Math and Music – Equations and Ratios
Previously in the “math and music” lesson we derived equations for expressing intervals as functions of relative frequencies. This week we’re going to define conventions for interval sizes and then derive three variables where we can determine the composition of any frequency ratio. Guess what – all intervals can be described as different combinations of the octave, perfect fifth and major third – the first three overtones.
In the last lesson we talked about the frequency ratios of common intervals. The standard convention is that interval ratios are greater than 1 and less than 2. A ratio of 2:1 is an octave, so it makes sense that all the other intervals are defined to be smaller than an octave. Following the overtone series we get these basic ratios: 1:1 is our starting tone, 2:1 is an octave above that, 3:1 is a fifth above the octave, 4:1 is the second octave and 5:1 is a third in the second octave. We want to express the fifth and third as frequencies within the first octave – therefore the ratio has to be greater than 1:1 (our starting tone) and less than 2:1 (the octave). Therefore, we can divide the frequency ratio by the number of octaves necessary to bring it into the first octave range. For example, the 3:1 ratio is a perfect fifth in the second octave. Therefore we only need to bring it down by one octave to have the ratio be between 1 and 2. So if a fifth in the second octave is 3:1 and the second octave is 2:1 then 3:2 would be a fifth in the first octave. We can define this as the following:
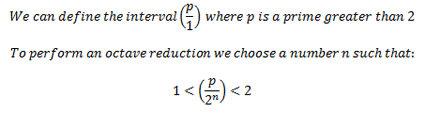
This equation shows how a prime ratio can be transposed into a single octave. From this equation is follows that:
![]()
Therefore we can frame the precise definition for our interval ratio as follows: a basic interval is an interval whose ratio is p divided by two the n-th power, where p is prime and n is chosen so that 2 to the n-th power is the greatest power of two less than p. The first three basic intervals from this definition are consonant and very important in the foundation of our musical definitions: the octave, perfect fifth and major third, 2:1, 3:2 and 5:4 respectively.
We’re going to set some variables based on these intervals. These variables will make it easier for use to define complex equations later on. Remember that the size on an interval is the logarithm of its ratio (see the “Math and Music – Intervals” lesson). Therefore we can define the following variables, a, v and t:
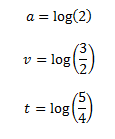
Now that we have those three variables defined, we can prove a method to determine the composition of any other interval as a combination of those three. Here’s how it will work: we’ll use three new variables, m, n and q to multiple against our originals (a, v and t). The sum of these will be the size of the unknown interval we’re trying to determine.
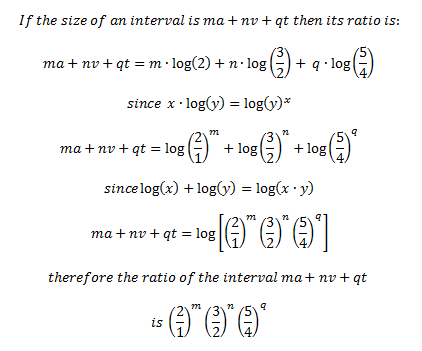
To give an example we can now express intervals as functions of a, v, and t and determine the ratios quickly – such as the sum of a perfect fifth (v) and a major third (t):
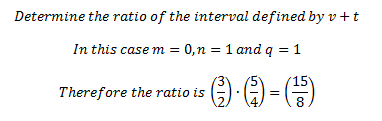
This can go both ways:
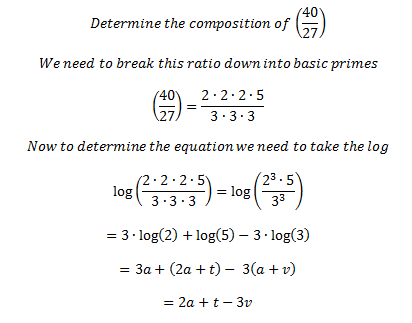
This means if we start at some pitch – any pitch – go up two octaves (2*a) then up on major third (t) and down three perfect fifths (3*v) we’ll end up at a pitch whose ratio is (40/27) multiplied by our original pitches value. This may not seem like much at first – but we’ve formed a precise language for describing interval relationships and calculating the composition of any interval from our fundamental values.
This is great in terms of raw theory – but how does it come into play with how we tune our instruments or understand music? It has to do with the value of measurement applied to the intervals and logarithms. We’re going to define that value based on Western equal tempered tuning. In our definitions of a, v and t we did not specify a base for the logarithms. Let’s define a base b such that the following is true:
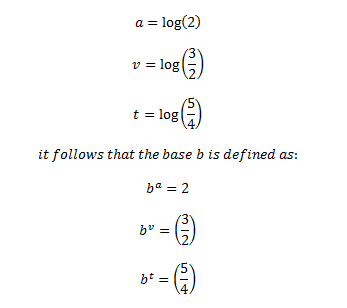
Let’s think of (b/1) as the frequency ratio of an interval. Therefore, the sum of a intervals having the ratio of (b/1) is the interval whose ratio is 2 – an octave. The same applies for (3/2) and (5/4) – the sum of v intervals with the ratio of (b/1) would be (3/2), and the sum of t intervals with the ratio of (b/1) would be (5/4). Therefore b is a unit of measure! In equal tempered tuning each note is an equal division of the octave – 12 chromatic tones in an octave mean that each note is (1/12) of the interval value of the octave. We can define this as follows:
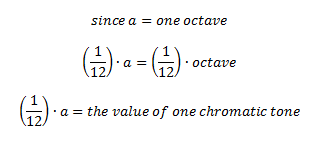
In music we often talk about cents a cent is based on this value of (1/12)a – it is one one-hundreth of the size:
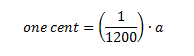
All of our logarithms are therefore defined with the base of the frequency ratio of a single cent. That ratio would be 2 to the power of (1/12oo):
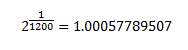
What have we accomplished? We now have:
- a method for describing any interval or its ratio in terms of an octave, perfect fifth and major third
- a concrete numerical value for tuning ratios (a definition of cents)
Believe it or not, this is how our music is defined – our intervals and the relationships between notes can be reduced to combinations of the first three overtones – an idea which is absolutely incredible when you think about it.




I believe I understand what you have done. How do we go about mathmatically understanding consonance? for example how can we mathmaticall predict a scale. The problem i find is in the +2 +2 +1 +2 +2 +2 +1 how can we use what you know to create a scale formula? can algarythms be formulated? can we predict consonance? is is all just what we like?
Neil – great questions! The answer is yes, you can mathematically deduce scales, though it’s not in the linear fashion you’ve described. It’s beyond the scope of a comment-post to go into full detail, but I’ll let you know that deducing a scale mathematically involves modular arithmetic around functions defined using the “a” “v” and “t” variables I outlined in the article. A good place to start is to read a little about the “Chinese Remainder Theorem” and then pick up the book “The Structure of Recognizable Diatonic Tunings” by Easley Blackwood. Good luck!
Great article. I am creating questions for a math and music “jeopardy” contest at our community college, and will try to use some of your lesson to make some questions. The tough part is keeping the questions below pre-calculus level.
Any suggestions?
Hey Russ – I would focus on the more direct-application math that would be more common-knowledge if you want to stay out of the heavy equation realm. For example:
1. What is the proper term for metric modulation? Answer = hemiola
2. What is the reference frequency for an A in equal tempered tuning? Answer = 440 Hz
Things of that nature, I would focus more on direct trivia than anything that would require derivation. Check out wikipedia for some high-level overview material that may be good:
http://en.wikipedia.org/wiki/Music_and_mathematics
oh no not an article trying to connect math with music! LOL! It’s almost like the math is trying to equate itself to some magic formula on making music. In my experience I have seen so many musicians go to the extreme of not learning to read music and saying rules stink and other musicians trying to use gimmicks and math to find the lost chord. I wish more musicians would just get back to basics of learning how to read music and learning how to play their instrument without all of this gimmick stuff. Just my two cents!
it’s so much easier to understand now…
6 out of 5 people can’t math .
I’m just going to go practice now………
music s gud…
I could follow the first paragraph or two, then my brain got full. May I be excused?
Evan, I just found your website, extremely interesting. I hack on the base but I am a math guy. so this article is forcing me to research music and music theory as I never learned theory, just played by ear. in your math progressions you are heading toward calculus or differential equations correct? as each note occurs x + 1 from another. I would like to see another article or discuss how one would write an equation for a music line.
Very original sounds examples of mathematic equation oriented music rendered with csound programming taken from a web tv show (in french).
– Mandelbrot set fractal applied in music using the 2 equations to render soundwave.
– Baby’s crying from parameters numbers only (not a sample)
– Great synth-like sound made with equation
– And finally a Techno song coming out of this simple equation –> y=sin(x^tan(x^sinx) )
See & hear it on http://tv.versatiles.biz/sujets/art_sonore.php
this doesn’t show an easy formula or equation that represents all music…. mathematically.
[…] See https://www.notreble.com/buzz/2010/02/18/math-and-music-equations-and-ratios/ […]
[…] of the cdim7 chord’s components, which constitute its unique and captivating sound. Picture a musical equation, with the root note serving as the foundation, harmonizing with the minor third, diminished fifth, […]