Math and Music: Intervals
Every musician should have an idea of the foundational concepts that allow us to create music. This lesson series will explore the basis for tonal structure in Western music.
I’ll warn you right now, this lesson is not for the faint of heart, or math-phobic. The purpose of this is to add to the conceptual foundation from which we view music with mathematical rigor. While there may not be a direct application of the theories presented in this lesson, it will change the way you think about intervals and tone. That in itself is valuable. If you are interested in diving into this topic more on your own a very complete explanation can be found in The Structure of Recognizable Diatonic Tunings by Easley Blackwood.
This lesson is the first of a few depending on interest – there is quite a distance to travel “down the rabbit hole” with the mathematics behind music, particularly in how we define a note, tunings, intervals and scale patterns. This particular lesson will focus on defining the calculation behind an interval. We are going to start with the loose concept that an interval is the difference between two frequencies, an unknown quantity. We’ll derive a method of assigning a real number value to that quantity for any set of frequencies, and then show how this can be applied to calculate other interval summations. At the end of this lesson you’ll know the mathematical basis behind a minor third and major third combing to create a perfect fifth.
Before we really start to dive in we need to define our initial reference point: the difference between two pitches. Think of two pitches (frequencies) which are separated by an arbitrary distance, i. Therefore if we have our two frequencies, f1 and f2, they are separated by the interval distance i1. We’re going to define the ratio of the two frequencies (f2 / f1) as r1. This can be expressed as:
![]()
If we have a second set of frequencies, f3 and f4, the interval between them can be defined as i2. The ratio of f3 and f4 (being f4/f3) would be defined as r2. If i1 and i2 are the same interval, meaning that the same frequency distance exists between f1 and f2 as well as f3 and f4, then the ratios will be equal. This does not tell us anything about the register of the frequencies, only that the intervals are congruent (we don’t know if they’re in the same register). We would express this as:
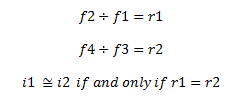
Let’s take another scenario – where we have three frequencies f1, f2 and f3. The interval between f1 and f2 is i1, the interval between f2 and f3 is i2 and the larger interval between f1 and f3 is i3. Applying the same concepts of calculated ratios in the previous examples we get:
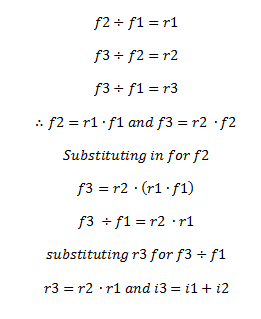
Therefore we show that adding intervals is equal to multiplying frequency ratios. This is a critically important concept for the next steps where we apply logarithms. For those of you that do not remember algebra, the logarithm of two multiplied values is equal to the sum of the individual logs of each value e.g. log(ab) = log(a) + log(b). Now we can do the following:
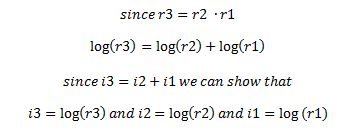
Now we have a defined number for the value of i. It is the log of the ratio of the frequencies comprising the interval in question. The frequency ratio for any given interval will be positive, but it may be greater than or less than 1. If the value of r is greater than 1, then we know that 0 < f1 < f2 and the interval is ascending (because f2 is greater than f1). Likewise if 0 < r < 1 then 0 < f2 < f1 and we know the interval is descending. Therefore the log of an ascending interval (with r > 1) will be positive while the log of a descending interval (with r < 1) will be negative.
So why is this useful? Well we know how to determine ratio of an interval formed from other ratios. For example, if we knew one interval (r1) had a ratio of 5/4 (which if you know your overtone series, you’ll recognize as a major third) and another (r2) the ratio 6/5 (a minor third) we can calculate the ratio of their sum. So a major third (5/4) plus a minor third (6/5) gives:
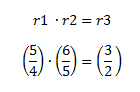
The ratio 3/2 is a perfect fifth. Do you realize what we just accomplished? We mathematically proved from a bare concept that a major third plus a minor third gives a perfect fifth! I admit, I’m a big math/music geek, but that’s awesome. A quick refresher for your small integer overtone pitch ratios so you can try some other examples on your own (I know you’re dying to, don’t pretend you’re not):

There you have it! Our first goal has been accomplished – we’ve taken the un-quantified concept of an interval, derived a real number value for it from the ratio of frequencies, and used our formula to calculate the ratio of a resultant interval. In the next weeks we’ll derive formulas to calculate frequencies, define what a note is, determine a method for finding the composition of any interval, and show that scale are modular functions (and how to use them).




Worth noting that we don't really use those interval ratios when we're playing as we use a pragmatic combination of well-tempered, pythagorean and natural tuning! But they're true for natural (but not fret based, or artificial) harmonics, of course.
This brings back fond memories of acoustics class back in college.
Learning to “lock chords” while playing with a group can be a lot of fun. While the human ear can't hear a 2cent change in pitch, they can tell when the fifth of major chord is dropped by 2cents and the third by 12 cents from equal temperament,. The inherent dissonance from the equal temperament dissipates, leaving a chord that is perfectly tuned.
I used to do this with sound generators in very vibrant rooms. My favorite was a large concrete room at the IX center. You can tune a chord to the frequencies of the room and hear the chord reverberate perfectly in tune for about a minute. A very cool experience.
Thanks for the comments! As bass players we can make use of the true ratios by playing the harmonic overtones on the strings – one of the many beauties of a non equal-tempered instrument. It begs the question of when it's better to play G# versus Ab ;)
This is the set-up into the next part – we can come up with a working definition of cent-value when we define the base of the logarithms and it works off the values of the first three overtones (2/1, 3/2 and 5/4) which does directly relate to how we measure equal tempered tuning.
[…] http://www.notreble.com/buzz/2010/02/04/math-and-music-intervals/ […]
AnyBody interested in this should read “On Sensations of Tone” by Herman Helmholtz.
AnyBody interested in this should read “On Sensations of Tone” by Herman Helmholtz.
A trick with numbers and tones, or how to find the natural scale with maths.
http://botverse.com/music-and-mathematics-findi…
I’m sorry, but you’re confusing mathematics with numerology.
As seen here, the relationship between notes of a scale is geometric, not linear as you state. All the rest is pure chance.
I’m a bass player, but also a former PhD student in mathematics.
This (well written) article, mathematically speaking, proves absolutely nothing.
For instance:
a) i3 = i1 + i2 is an assumption here, is not derived from above
b) “we can show that i3 = log(r3) …”. No, you can’t since the intervals were defined by an equivalence relation
Finally, nowhere in this article explains why the ratio of an octave is 2/1, much less why is 5/4 a mayor third.
I’m not saying that all the statements are wrong, which aren’t, just that the math behind the speech says nothing. At least to me.
Hey Franco –
Thanks for the input, if you’re interested in the full derivations I suggest you read “The Structure of Recognizable Diatonic Tunings” by Easley Blackwood, there is exhaustive proof of what I’ve barely touched here.
Admittedly I am not a math scholar, so my very brief summary of Blackwood’s concepts may not be as rigorous or precise with the language for definitions (it’s the inherent risk of condensing two huge chapters of a book down to one small overview article), but I am able to appreciate the beauty of the underlying system of music in a different way because of his work. My hope was to give other bassists a glimpse of that beauty, even if it was through slightly blurry glasses ;)
This is a really cool way to say what we play! I am not such a math wiz, but Music theory is like breathing for me. This article points out a really cool perspective of how human beings try to rationalize the divine, which I believe Music is.